At a glance
Introduction to Transmission Modeling
A model is a simplified representation of a more complex system or process. Infectious disease models can support outbreak responses by providing insights into how diseases may spread through populations, projecting the size of outbreaks, and evaluating the potential impact of interventions. Transmission models, a category of mathematical models of infectious disease, represent transmission and progression of infectious disease through a population. Transmission models are mechanistic, meaning they use equations to represent the processes underlying disease transmission. At a minimum, they represent the process by which infectious individuals infect others. However, the complexity of transmission models varies greatly – ranging from a single equation to describe transmission across an entire population to detailed representations of each person as an individual element within a population.
The equations of a mathematical model use specific values, or parameters, that represent the various characteristics of infection and of the population. These characteristics can include the number of contacts an average person has with other people, the likelihood of infection given contact with someone who is infectious, and the duration of infectiousness. Model structures and parameters can be adjusted to create scenarios representing public health interventions (e.g., vaccinations that increase immunity or treatments that shorten the amount of time a person is infected) or pathogen evolution (e.g., a new variant with a shorter incubation period). Comparing model output from these scenarios can provide understanding into how each factor affects disease transmission, which in turn can help with planning, preparedness, and public health decision-making.
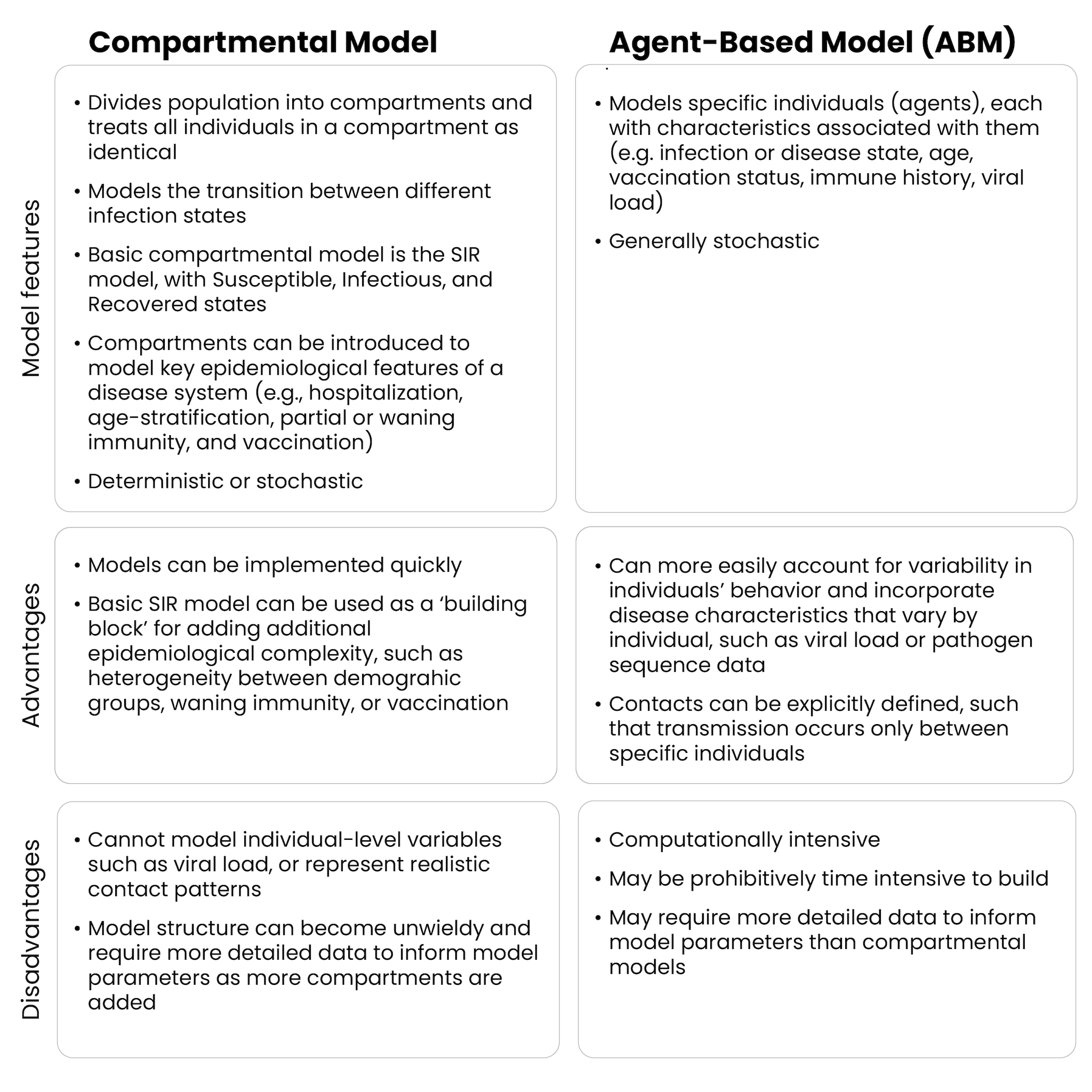
A single model can combine various methods, depending on the specific goal and purpose. However, many transmission models fall into two general categories: compartmental and agent-based. Each approach has strengths and weaknesses, and understanding them can lead to more effective decision-making during outbreaks.
Compartmental Models
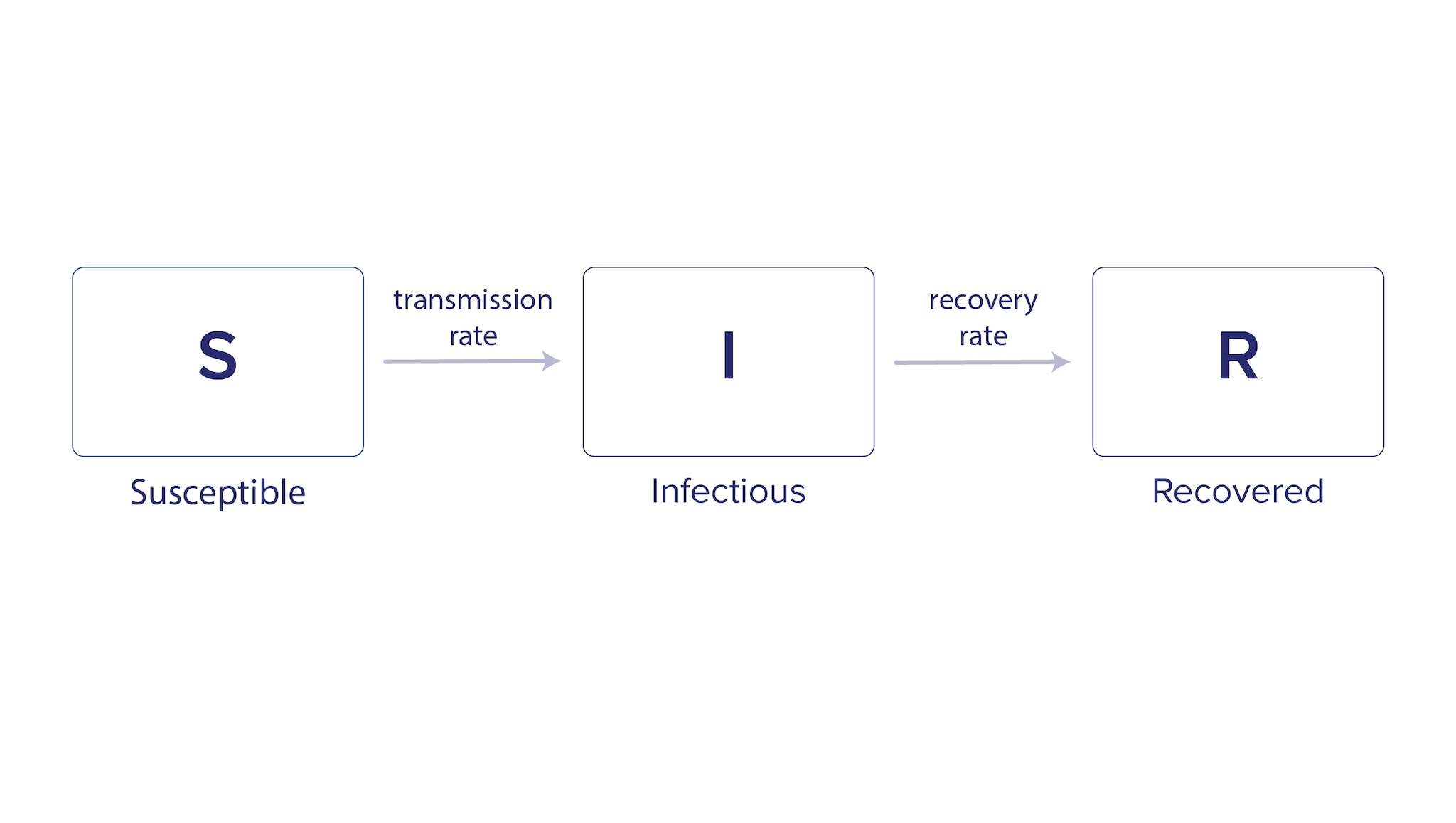
Compartmental models group the population into categories, or compartments, based on infection status. The model uses equations to describe how groups move between compartments. A common example of this type of model for infectious diseases is the Susceptible-Infectious-Recovered (SIR) model, which represents the population in three compartments based on infection status (Figure 1).
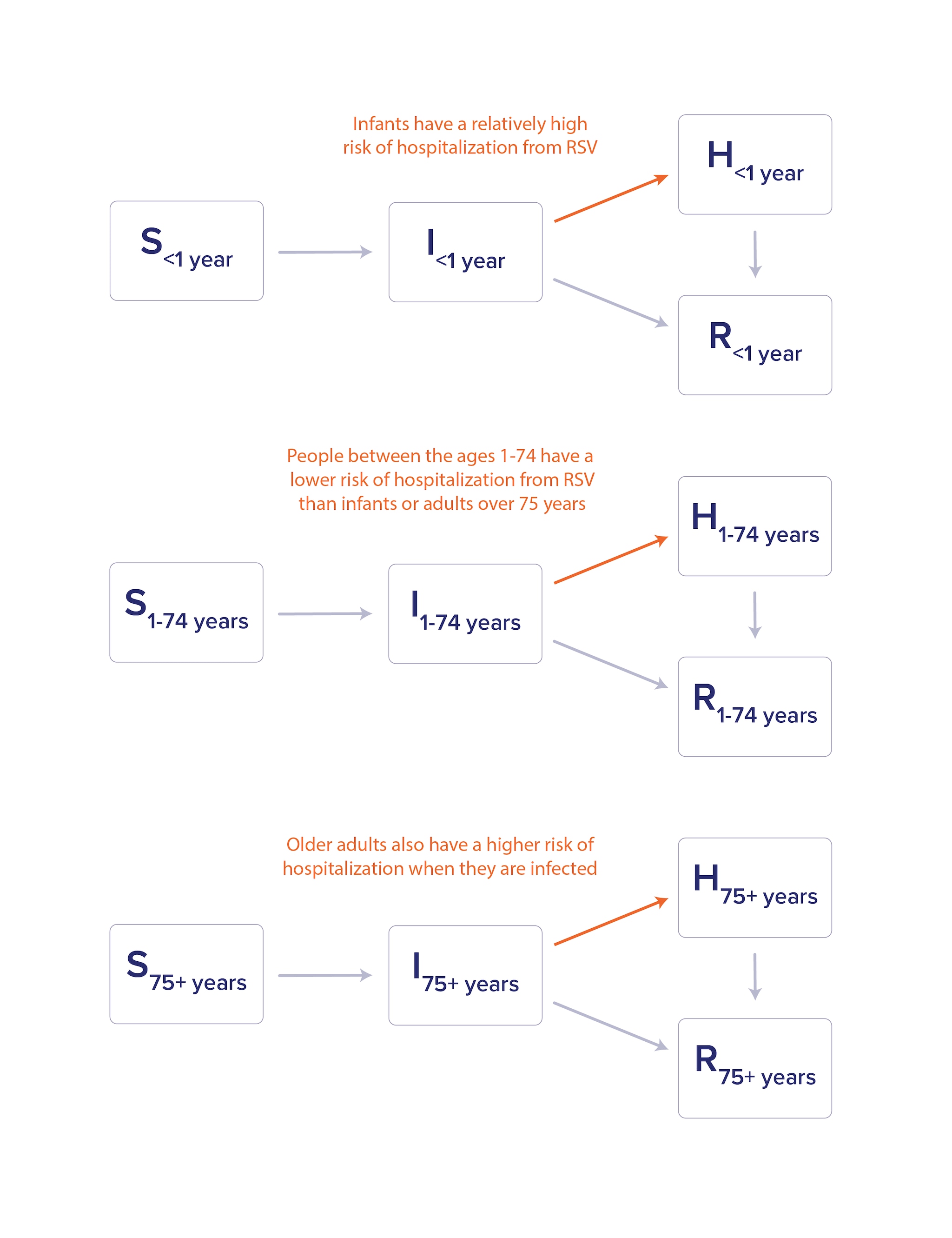
Compartmental models can include additional complexity to more accurately depict the disease transmission they are trying to represent. The age structure of a population is one characteristic that can be important for infectious disease dynamics. For example, the disease caused by respiratory syncytial virus (RSV) primarily causes hospitalization in infants and older adults. In a compartmental model for RSV that accounts for hospitalization (H), incorporating age structure would allow for different hospitalization rates based on age (Figure 2).
Compartmental models can incorporate the effects of vaccination, which may include protecting the vaccinated individual from infection or disease as well as reducing transmission to others. Model structures can capture changes in infectious disease dynamics for those with partial immunity from vaccination or prior infection versus those with no immunity (Figure 3a). These models can be constructed to incorporate different types of vaccine efficacy as well as waning immunity (Figure 3b). As with hospitalization rates, vaccine waning and efficacy can vary by age or other characteristics, and model structures can also reflect these complexities.
Adding real-world details can quickly result in a very complicated series of compartments within the model. Increasing model complexity can add to the time needed to develop, test, and deploy the model, increase the amount and types of data required to parameterize the model, and make the results more challenging to interpret. For these reasons, modelers often aim to use the simplest model that still captures the necessary complexity of a system required to answer the public health question of interest.

Deterministic vs. Stochastic models
Another important characteristic of compartmental models outside of compartment structure is whether they are deterministic or stochastic. In a deterministic model, parameters describing probabilities – like the probability of infection after a single exposure or the probability of hospitalization in infected individuals – are treated as fixed rates. As a result, the model produces the same result each time it is run for a given set of input parameters. For these models, uncertainty in model predictions is quantified by accounting for uncertainty in model inputs (i.e., running the model with a range of parameters). Consider the age-structured model shown in Figure 2: while we know that infants and older adults are most likely to be hospitalized with RSV, the precise likelihood of hospitalization for infected infants or older adults may be uncertain. Published literature often provides a plausible range of values, so modelers might run the model multiple times using different hospitalization rates from that range for each model run.
In contrast, in a stochastic model, random variation is built into the model, and each simulation represents one potential outcome of a random process. For example, in a stochastic SIR model, the number of new infections in each time step can be determined randomly as a function of the number of current infections, the number of susceptible individuals, and the per-contact infection probability. As a result, each simulation produces a different outcome. The model is then run many times to produce a range of possible outcomes, providing estimates of outcome uncertainty.
Stochastic models can be especially useful in small populations or during the early stages of an outbreak, when random events can substantially impact the total size and speed of an outbreak. For example, the first infectious person in a population might, due to random chance, interact with zero people while they are infectious (i.e., if they stay home) or 20 people (if they go to a social event). These two scenarios can lead to very different outcomes in terms of whether or not an outbreak starts. Stochastic models have the ability to capture this variability. In contrast, deterministic models cannot account for these types of random events. However, deterministic models are more computationally efficient and are often sufficient when outbreaks have grown large enough that random variation has less impact on disease spread.
Agent-based Models
Compartmental models can capture various population characteristics, but the total number of compartments can grow rapidly. In cases where modelers might need to incorporate many individual-level characteristics in a population, agent-based models (ABMs) can be beneficial. ABMs simulate disease spread at the individual level, where each individual, or "agent," represents a separate entity with its own characteristics, such as age, vaccination status, and disease status (Figure 4). ABMs, like compartmental models, have a mechanism for disease transmission, but instead of applying it to groups, transmission happens at the individual level. In an ABM, each individual can interact with other individuals and have unique behaviors that affect disease spread, allowing for more detailed simulations.
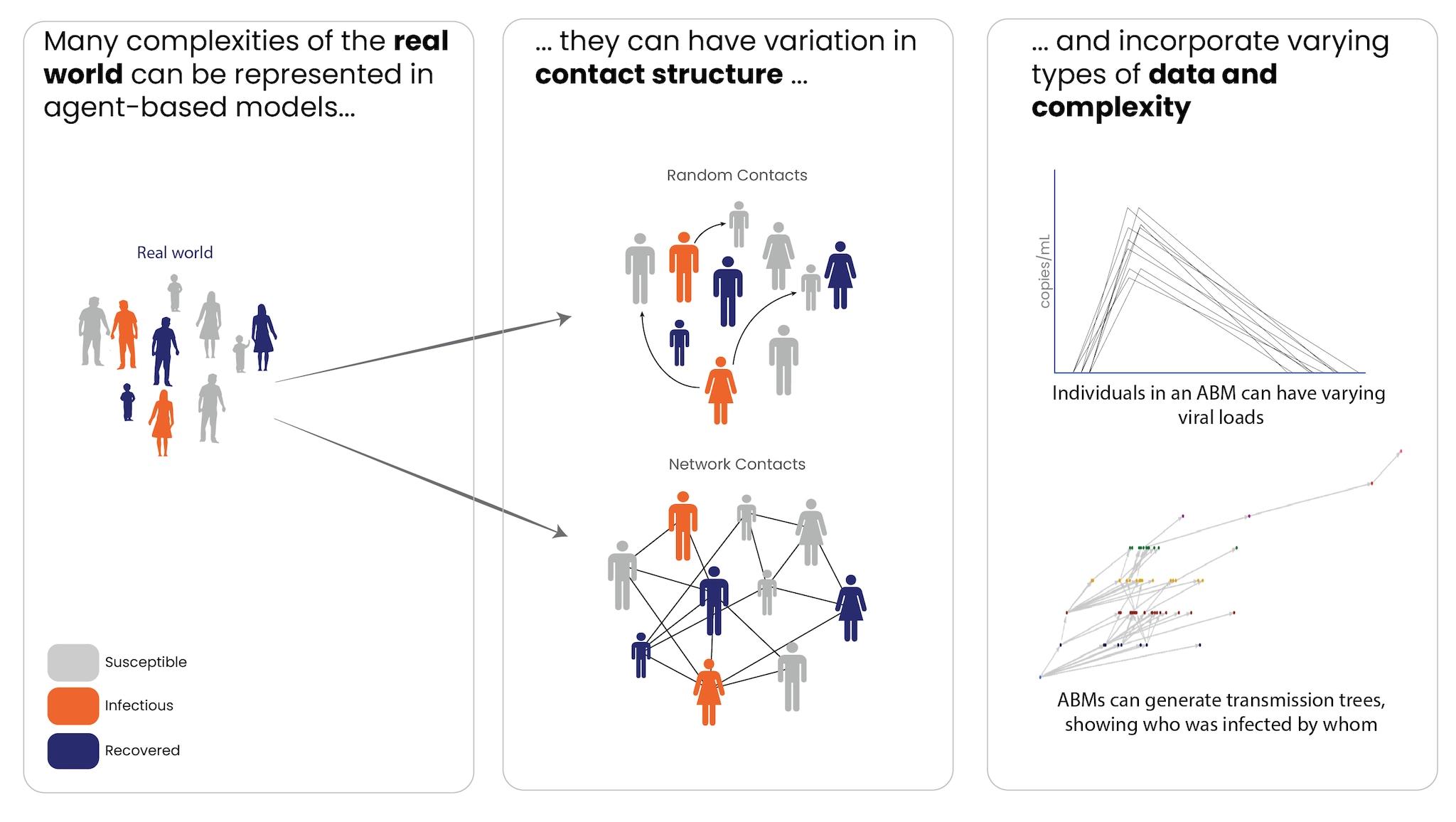
Because ABMs model at the individual level, they can more easily account for variability between individuals' behavior and change underlying assumptions in individual-level characteristics. ABMs can be valuable when individual-level variation (e.g., age, mobility, social behaviors) is important to disease spread. They can also incorporate disease characteristics that vary by individual, such as viral load or pathogen sequence data.
ABMs can also provide more flexibility when it comes to modeling contact between individual people, which has particular relevance to the transmission of infectious diseases. They can simulate random contacts between people or can be applied to a network, with specific contacts between individuals. When interactions depend on social networks (e.g., in households or schools) or other factors, ABMs are well-suited to capture these dynamics. This flexibility allows ABMs to model individual-level interventions, such as contact tracing, and generate data – like who each infected person was infected by – that compartmental models cannot.
ABMs are generally stochastic, meaning that, like stochastic compartmental models, individual runs of a model are different and the model must be run many times to produce a range of possible outcomes. However, unlike in a standard stochastic compartmental model, modelers using ABMs can define individual-level transitions between disease compartments. This allows for more precise control over the structure of an ABM than in a typical compartmental model.
This level of granularity and specificity can come with drawbacks. ABMs are complex and typically require more computational power, generally making them slower to both design and run. The increased complexity also means that more data is usually necessary to validate and parameterize the model. For example, to specify the age, vaccination status, or likely mobility patterns of each individual "agent" in the model, modelers need a very detailed understanding of the population. For these reasons, using ABMs in a response framework may be most appropriate when aspects of the model, such as demographics and the contact structure, are readily available or have already been tested prior to an outbreak.